Retrieval on Parametric Shape Collections
Abstract
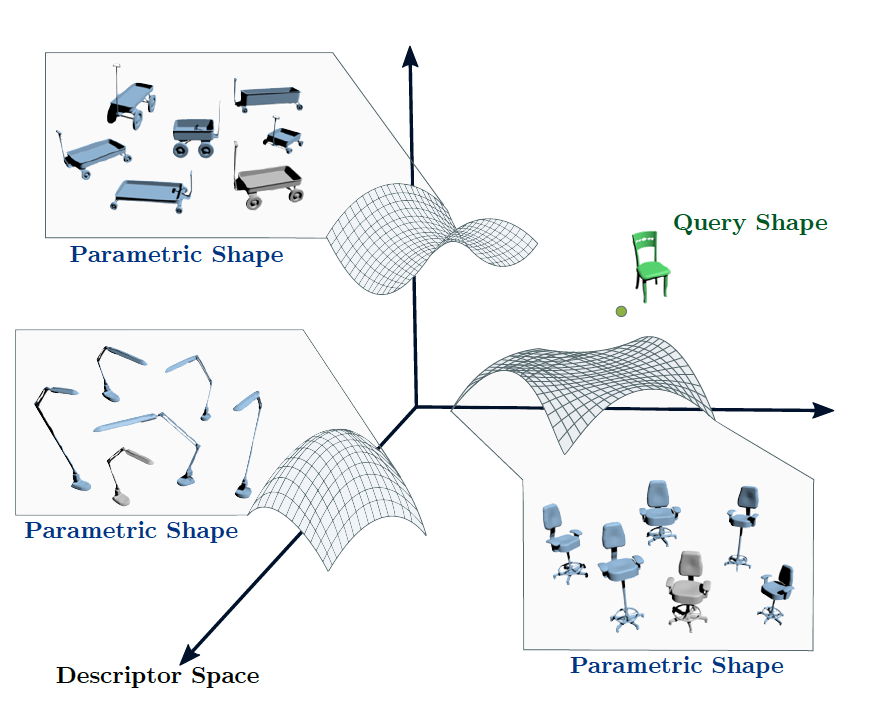
While collections of parametric shapes are growing in size and use, little progress has been made on the fundamental problem of shape-based matching and retrieval for parametric shapes in a collection. The search space for such collections is both discrete (number of shapes) and continuous (parameters values). In this work we propose representing this space using descriptors which have shown to be effective for single shape retrieval. While single shapes can be represented as points in a descriptor space, parametric shapes are mapped into larger continuous regions. For smooth descriptors, we can assume that these regions are bounded low dimensional manifolds where the dimensionality is given by the number of shape parameters. We propose representing these manifolds with a set of primitives, namely: points and bounded tangent spaces. Our algorithm describes how to define these primitives and how to use them to construct a manifold approximation that allows accurate and fast retrieval.We perform an analysis based on curvature, boundary evaluation, and the allowed approximation error to select between primitive types. We show how to compute decision variables with no need for empirical parameters adjustments and discuss theoretical guarantees on retrieval accuracy. We validate our approach with experiments that use different types of descriptors on a collection of shapes from multiple categories.