Qualitative Organization of Collections of Shapes via Quartet Analysis
Project PageAbstract
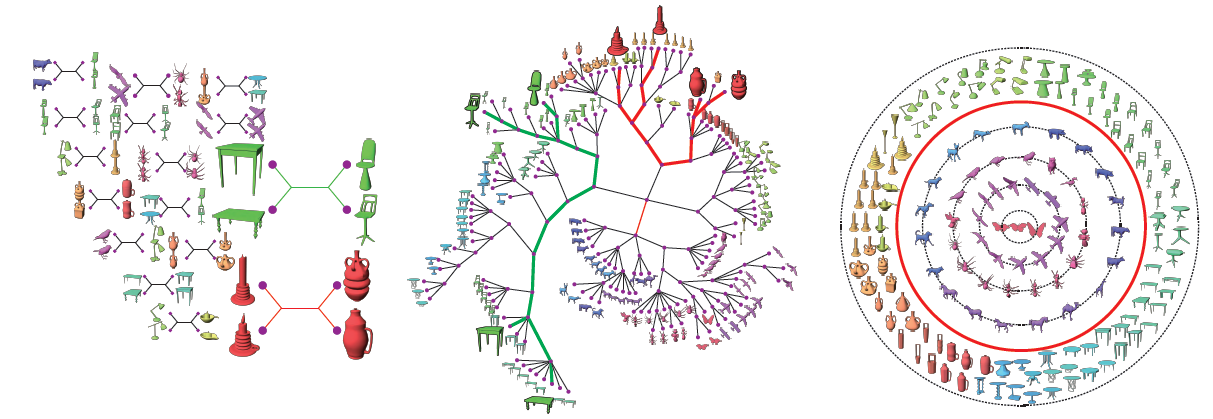
We present a method for organizing a heterogeneous collection of 3D shapes for overview and exploration. Instead of relying on quantitative distances, which may become unreliable between dissimilar shapes, we introduce a qualitative analysis which utilizes multiple distance measures but only in cases where the measures can be reliably compared. Our analysis is based on the notion of quartets, defined by two pairs objects. In each pair the shapes are close to each other, but far apart from the shapes of the other pair. Combining the information from many quartets computed across a shape collection using several distance measures, we create a hierarchical structure we call categorization tree of the shape collection. This tree satisfies the topological (qualitative) constraints imposed by the quartets creating an effective organization of the shapes. We present categorization trees computed on various collections of shapes and compare them to ground truth data from human categorization. We further introduce the concept of degree of separation chart for every shape in the collection and show the effectiveness of using it for interactive shapes exploration.